Place Value
With
Base 10 Blocks
Place Value Made Simple.
Place Value with base 10 blocks is fun and easy.
Here is a blog post covering "more advanced" place value from one out to millionths and clearing up the common question "why are there no one-ths..?" We will also talk about getting a grasp of large numbers, which is sorely needed in today's world. This concept along with 'the law of large numbers' is what prompted me to build this website, by the way.
Meantime, as usual, we will start at the beginning, with lessons for little children and work our way up. Teaching place value with base 10 blocks can be considered a preschool math activity! But of course you can use it on 1st and 2nd graders too. They all like to learn place value with base 10 blocks because it make the experience fun and easy.
I like to start with a lesson on place value with base 10 blocks using 111. Click the picture for a quick explanation of what's going on here.
I start with 111 because it instantly exposes students to the concept that each number can mean something more than just one.
Universally, each very young student who is exposed to 111 on a page or white board will tell you with all certainty that that's the same as three. If you happen to bump into a very old Roman they would agree, but we are teaching place value with base ten blocks & base ten mathematics. We have come a long way since then. Hmmm, I even write 111 = 3 sometimes.
"Is that true?, How do you know?"
You will get some variation of "Because one and another one and another one is three...everybody knows that!"
"What if I told you that this means something else?"
Get out one hundred, one ten, and one unit. The draw a picture of each, then write 111. Teaching place value with base 10 blocks is EASY because it makes it visually obvious that those ones are not all the same.
"Study this for a second. Those symbols mean those blocks."
"Which one do you think means the 100?"
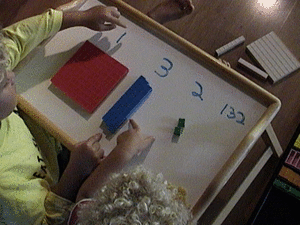
They may or may not get it...if they give you the wrong answer give them more information. Remove the no from the lesson. If they point to the one on the right (the ones place) ask, "do we read left to right or right to left?" You may need to clarify by pointing with your finger and sweeping left to right as you say it. "This way or that way." The student may not know what you mean by "left to right".
You may also correct them by telling them what they ARE pointing to..."that's the ones place".
"Really. Each number means something depending on where it is. The numbers tell you how many; the places tell what kind. Can you remember that? Each number has two parts: the what kind part and the how many part. WE COUNT THE BIG ONES FIRST"
"Okay."
"Simple enough; lets play. I'm going to give you the secret code and you have to get out what the code says..."
"Okay!"
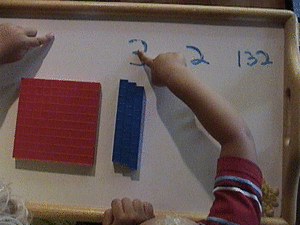
First, I put the the super secret code on the top of the board. 1 3 2. Then I put it on side where it looks more like a proper number, 132, we are going to draw it too.
We started in the concrete: they know the names of the blocks, now it's just counting...and doing some addition and subtraction by counting and they learn place value to boot.
After they got out the right blocks with no help from me we have a little fun and I ask them to point to the tens and the ones and the hundred etc. Then the super fun part where they get to use their fingers to erase the numbers.
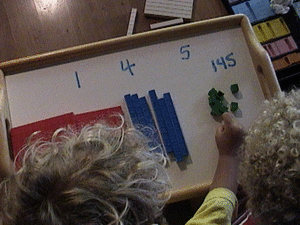
Erasing is the "funnest" part of the place value with base 10 blocks lesson. They've already erased the drawing part and are working on the other parts. You and I call it a lesson they call it a game. They are having fun. Now a new secret code...how much more fun is "secret code" than "problem"? 145!
Keep in mind they are getting no help from me, I may ask a question now and then but for the most part they are doing it all by themselves. I obviously need video...in time there will be.
You can see they got a new place value code so they got lots of blocks out...they have two hundreds, 6 tens and 7 ones because, as any little can tell you, 5 is "a lot."

So at this point I offered encouragement and asked a couple questions.
"Very good! You guys got out lots of blocks! Is that what the code says? Do you need all of those blocks?...You better count it to make sure."
The older boy gets rid of one of the hundreds, and then separates the tens: he didn't count all of them, he just pushed the other two away when he got to four. The younger boy, to my surprise, began getting rid of units, the right amount of units...and then got rid of the two tens...
"Toooo many!" he said.

Now it was time to count it again just to make sure. I didn't ask them to count it again, they did it. As he counted, he related the symbol to the block and made sure his brother was following along.
Then he got the extra hundred and gave it to his brother, "here: we don't need this one do we?" (the younger boy was the one who got it out in the first place). Place value with base ten blocks.
"No we don't. I'm sorry."
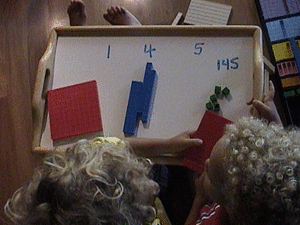
Now it's time to point to the various elements. Show me the 100, then show me one ten , how about four tens...where's the symbol for 4 tens? Etc.
I sped it up so they could hardly keep up and we laughed as we did it: 4 tens, 1 hundred, 5 units, 40, 100...!
Place Value with base 10 blocks in the classroom.
If you are teaching place value with base 10 blocks in the classroom, one of the games in a larger class can play is where one student on the team holds up a block for the teacher to see and they point to the symbols on a handout that has numbers on it. All the students on the team would point to the symbol representing the block the student is holding up and say it. The students take turns holding up the blocks alternating between pointing to the number when a student hold up a block or holding up a block when a student says or points to a number on the big board at the front of the class. If they hold up the wrong block allow them to look around the room and see if everybody else is doing the same thing, if not, they can self correct. If you have to, tell them what they have and what you want. Do not say, "no that's not right": remove the no from the lesson.
Teams of two, three or four depending on available blocks and number of students can be made. Keep in mind banker, builder, drawer, recorder. In this game I am the drawer and recorder and and the boys are the banker and the builder...
Banker gets out blocks, builder puts them in the right places, drawer would draw it, recorder would make the symbols. For older students kindergarten, 1st grade or 2nd grade you could say the secret code ad they could do all of the work, or you put the code on the board and they make the problems..the code could be symbols or drawings...the boxes lines and dots really do look like secret code.

Again, this shot is posed but you cannot manufacture or fake the looks of genuine satisfaction on their faces. They did it all by themselves. They have received heaps of praise. They feel good about themselves and math, place value is not hard or confusing but visually obvious. At this age (unlike teen-agers) they want to please you. Pu them in a situation where they can not fail. The cruelest thing a teacher can do to a student is put them in a situation where success is less likely than failure at this age. It makes my blood boil. Sometimes the teacher is well meaning but misguided, trying to give a "challenge" too early on. Other times the teacher and sometimes the parent is just mean spirited...these kind of people make me want to hit them repeatedly with a stick.
Let us continue, I'm sure none of this applies to you.
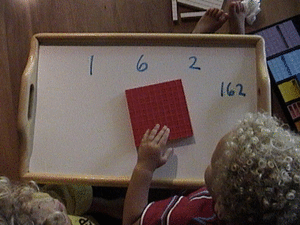
For our next place value with base 10 blocks adventure: 162. We started with a clean slate. Sometimes you leave the pieces there and they have to add or subtract other times you start fresh. Starting fresh is a lower degree of difficulty. Just play: there's no wrong way to do it.
Because the younger one was showing some acumen, I gave him a problem to try by himself, his brother was instructed to only help if he was asked for it.
The one hundred was easy. The tens presented a problem because he did not, at this stage, have a one to one correspondence 100% developed. So he asked for help. His brother was happy to count the blocks and tell him he needed "more."
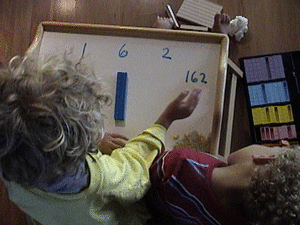
He did not specify. He did count the blocks one by one out loud for him.
"One, two, three, four." ["Julian" is the Cypher.]
"But I want six!"
"More."
Now we have six...and they count it several times to be sure. This is cooperative learning at its best. We also incorporate VAK. Plus whole brain learning. The whole ball of wax. Hence the name Mortensen More Than Math.

Teachers are then shocked and amazed at how quickly students learn math concepts. They are also amazed that the next day they have to start all over again because they seem to forget overnight what they just learned the day before: even when mastery is demonstrated the concepts must be reinforced with repetition.
One thing you may notice when you do a lesson over and over again and then drop it for a week or two suddenly it's "in there" and the student knows it without thinking much about whatever it is. The subconscious mind has digested it and pathways from storage to retrieval have been built, especially if the mind knows it will be of use later. Remember 18 impressions minimum to build the pathway from the sub conscious to the conscious for ready recall. There are many other ways around this but we won't cover them here. Take a look at my Blog post called "House for a Duck."
The next part is easy because the youngest boy knows how many two is. And he gets them out triumphantly.
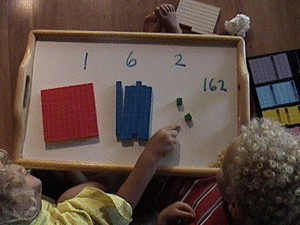
And now it's time to point to the various parts, Here the older boy points to the 2 units.
I ask them what the two means: they say, "units". I ask them what the one stands for: they say "100!" Show me 60...they do so, all without error which means we've come close to mastery. Being able to do place value without error is great, mastery is exhibited when they can make problems for you...and tell you if you did it right or wrong. Hint: ALWAYS get a couple wrong and ask for help. If they give you 237, for example leave out something and see if they notice. They ENJOY correcting the teacher...
Here I managed to remember to take a picture of the drawing for this place value code. ALL the problems above were also drawn (and erased which is the fun part) and here the youngest is about to erase the picture of the 100.
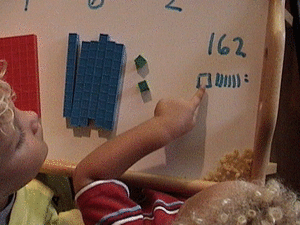
Now we've been doing math for a good 30 minutes. Be mindful of quitting while they are still having fun.
You should hear "Awww...." or some other protest, ideally.
Lastly before cleaning up the place value lesson we erase the numbers. I'm not kidding, universally this is the funnest part for kids all the way up to about second grade. It's a reward to be able to be the one who gets to use their finger to erase.
Previous to this we had done a few three period lessons identifying the blocks. Then we did a few three period lessons where we compared 7, 17 and 70, as well as a few others like 3, 13 and 30, and we were on quite a roll because they really didn't want to quit.
So we changed the lesson from place value to building rectangles and counting the sides. Some days are diamonds others coal. There are times when I suggest we play math and they are enthusiastic, other times when they say they don't want to. Days when, like this, an hour flies by, and other times when it's OBVIOUSLY time to quit after 5 or 10 minutes. Try again later or wait for a day...with young kids everyday really is a new day because they have very little concept of time. This is because their brainwave activity is not beta but alpha...or even theta...until they are six or so they are basically in "download mode."
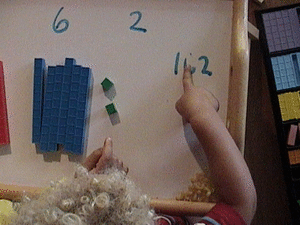
Place value is a HUGE accomplishment of man's mind. Teach place value with base ten blocks or manipulatives to make it easy to understand. It has taken us thousands of years to get here. We take it for granted now, but there was a time when we didn't use place value and that made it pretty hard to count. Place value definitions out of text books are amusing:
"Place Value signifies a positional numeral system...one of the the earliest systems of written symbols is found in ancient Mesopotamia which was a system of symbols for numbers.
Modern numeral systems are place-value systems—that is, the value of the symbol depends upon the position or place of the symbol in the representation; for example, the 2 in 20 and 200 represent two tens and two hundreds, respectively. Most ancient systems, such as the Egyptian, Roman, Hebrew, systems DID NOT include place value which complicated computation..."
"Complicated" is an incredible understatement.
KISS: the numbers tell you how many the places tell you what kind. Keep it simple.
"Maya mathematics included two outstanding developments: positional numeration and a zero. These may rightly be deemed among the most brilliant achievements of the human mind. The same may also be said of ancient Maya astronomy. The duration of the solar year had been calculated with astounding accuracy..." from the encyclopedia Britannica, The Maya Calendar and Writing System
Make no mistake we only teach concepts that have already been discovered but we ought not forget the incredible journey the human mind has taken to get here...directing the discovery of these concepts is so important that English words are barely adequate to express just how important it is: let the child discover the concepts again for themselves.
They will figure out "it never goes past nine" for themselves. If they try to add more units or tens (or hundreds or...) than nine they have one of the next kind and it goes in the next place over...let them discover this for themselves!
Now, as we stand in awe at the alter of the mathematics, what is wrong with this picture?:

Hint it has to do with the dots...they are the same for ones, tens and even thousands. Anybody else see a problem here? Or is it just me...? And why didn't that boy put zero in there?
This page was built before I had a video camera or knew how to upload video to the internet. It wasn't that long ago when webpages didn't have videos on them...Because there weren't any. This page is from that era, As you can see Dboyz were very little back then.
But now I have all manner of devices that the digital recordings:
This is a great video because it shows a lesson in action, and the transition from ignorance to understanding. This is a completely normal response when they're little and don't understand place value quite yet...The concept is simple: the places tell you what kind and the numbers tell you how many. Any little child can understand that numbers have two parts: the "how many" part and the "what kind" part.


Crewton Ramones No Mystery Theatre.
FREE! Addends App.
Counting With Base Ten Blocks
“She doesn't understand the concept of Roman numerals. She thought we just fought in world war eleven.” ~Joan Rivers
"Learning without thought is labor lost." ~Confucius
Confucius: one of the greater mathematicians. People forget the relationship between the mathematics and philosophy.
"The pupil can only educate himself. Teachers are the custodians of apparatus upon which he himself must turn and twist to acquire the excellencies that distinguish the better from the poorer of God's vessels." ~Martin H. Fischer
