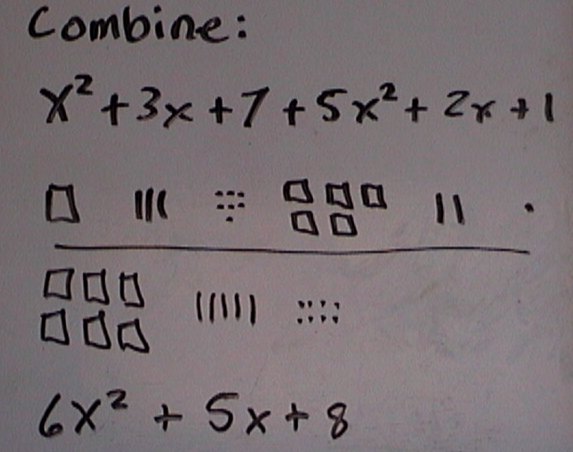|
Math Terms = Math Vocabulary.Math is a simple beautiful language. Pity we don't teach it that way. Math terms are often a source of trepidation and fear.Soon this page will have links to a glossary of math terms: math vocabulary and definitions. But here at Crewton Ramone's House of Math Math you will actually understand them because they will come with pictures and visually obvious explanations. Vocabulary will be roughly divided into groups for the grade level teaching some of you may be more familiar with, since publik skoolz insist on segmenting everything. Segmentation is fine, there's nothing wrong with bite size pieces unless the bites are so small and disjointed that they student lose the meaning and the math becomes meaningless, and therefore useless. The Mathematics has it's own vocabulary. Much like any subject, it has a "lingo". You need to know "the lingo". On a boat for example the toilet is called "the head", toward the back of the boat is "aft" once you get there you are at the "stern", the front "fore" and the ones everyone always confuses are port and starboard for left and right, the light on the port side is red the light on the starboard side is green. It's just vocabulary. Why do math term cause fear? Why aren't people afraid of boat vocabulary? We start by naming symbols often times. This is a 1, one...this is a two. But we can also count things and call two flowers two or 3 dogs three... If we start by naming blocks the little green one represents one, the orange one two and so on. These are math terms but not exactly what we're talking about. When people think of math terms they think of x2 or x3 or maybe Pythagorean Theorem; however the first math terms are the names of the numbers. Counting one thru nine is easy and fairly natural. Add one more and you get ten. 10. Now we can introduce the simple concept that a number has two parts. The "how many part" and the "what kind part". Some numbers like fractions tell you right there in the symbol...2/3 for example tells you two of the thirds kind. 10 tells you one of the tens kind. 11 is one ten and one and it has a name: eleven. Many students start with "one ten and four" and then move to fourteen which is the proper term for 14. We use a three period lesson to introduce new concepts or vocabulary. Here we see a simple three period lesson where we are just naming 7, 17 and 70.

First we counted out 7 pieces of macaroni. (The "this is" part of the lesson.) Then 17, then we talked about which blocks would be the best to show 7 and 17. Then we talked about but did not count out 70 pieces of macaroni it would have taken too long and they would have lost interest...that's why we have multiple ten blocks: one block is 7 tens (or 10 sevens) and you can grab it fast. This way we don't lose track of the concept. "If these were jelly beans which would be the most?" He's holding up the 70 for all reply. Note the younger student is not even three but he knows 70 is more than 17 or 7 even though they sound very similar. No concept is beyond the child if it is presented at the child's level.

Now we go back and fourth between the numbers on the table. I asked for 7, he grabbed the nearest one to him. The older student thought this was funny and wrong because that was the 7 from the 17. I said "very good!" To both of them. This simple praise works wonders. "You're both right. He's holding up a seven from the 17! You show me 7!"

Note the youngest is reaching for the seven again because he wants more praise too... We went back and forth: show me 70...point to 17...point to 70, point to 7...etc. Lastly, I ask "what is this" and I point to the 70, the 7 and the 17. I do it several times so they know it for sure. Don't kid yourself though you will have to do do this many times with each number before they "know it by wrote."

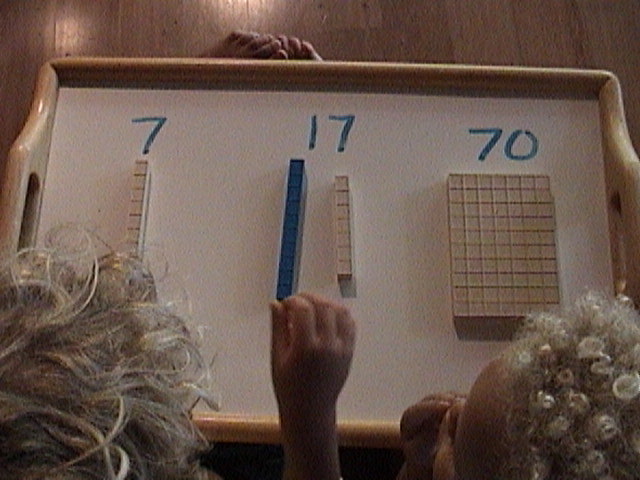
Now they relate the symbols to the blocks and have a feel for how many each number is. They have more than an abstract concept for each math term. After this shot the blocks were removed and only the symbols remained. It was still easy though.
Place value. (Place value is also a math term.) Now we can use a three period lesson to cross teach the names of the blocks and place value all at one. 111 ANY little kid almost can tell you that's three! One hundred eleven? That's ridiculous. Preposterous! Silly. But then you show them that the numbers tell you how many, the places tell you what kind and it begind to make sense. Here we see a simple three period lesson set up for 111. 
In the picture the younger student has correctly identified the ten but is erasing the symbol for the ones (or units). Note how he is using two hands for whole brain, kinesthetic learning. Little kids love to erase with their fingers on white boards. It's a fun math activity to erase the answers. I corrected the child by telling "him that's the ones place, I want you to erase the tens place." I re-wrote the one; he thought for a moment and correctly erased the middle one. Tell them what they have, not what they don't have; what they are doing and what you want them to do, not what they did wrong. And remove the "no" from the lesson. Very shortly they were conversant with one, ten and hundred AND their places. Next it was time to play games where they had to get out 132, 156 and 243 and so on. More on place value here. {link not built yet} Then we flipped them over and did x2, x and unit.
"Combining Like Terms"x2, x and unit The big red one is called "x-square", the blue ones are called "x" even if there's more than one we still call them "x" and the units are just units or numbers that we call by name...math terms are EASY. Use a three period lesson to introduce these blocks/math terms. Do this for the first few times even after they know them to keep it fun and easy. Be playful.

Can you see where combining like terms becomes child's play once the student knows the symbols can be represented by the blocks and therefore by drawings of the blocks? Here is I used color pens but crayons work well too. Little kids are allowed to use color if the want but older students use pencil only, otherwise it takes to long to draw and distracts from the concepts. Even just using pencil is to sketch the problems eventually TAKES TOO LONG and they understand why we use symbols: it's faster. You we see problems like these in text books: Combine like terms: x2 + 2x + 2x2 + 3 + x Adding x2 + 2x + 2x2 + 3 + x to get 3x2 + 3x + 3 is DUCK SOUP. Drawn it looks like this:
We are just adding stuff (math terms) that is (are) SAME. Now a problem like this is SUPER EASY. x2 + 3x + 4+x2 + 2x + 1 [] | | | :: [] | | . People see a problem like this and sometimes start to freak out. I put this problem on a black board for some seventh graders once and they began to protest "We're only in 7th grade!" We had already done a three period lesson on these math terms. So I said, "JUST DRAW IT. No whiners." "Oh..." And every kid in the class got it right. No long explanations about how "the coefficient one is understood," no muss, no fuss. No tears no fear. Just understanding of what was previously abstract algebra. Wait 'till you see how easy this makes factoring trinomials or quadratics. In order to do so, you have to understand the math terms and the blocks make that EASY. After a while it becomes so visually obvious they wonder why they have to draw it "twice". 3x2 + 4x + 5+5x2 + 6x + 7
What if we string the math terms out? STILL EASY. Older kids can skip the blocks and go directly to drawing them. But always start in the concrete and introduce the math terms with the blocks. What if we throw in a y or z? Make new drawing for the new variables. WE ONLY COUNT STUFF THAT IS SAME. With the younger kids we can use different color blocks or just mark the blocks to represent y's and z's, I get really tricky and mark them with...y's and z's...but petty soon all they will need is symbols not drawings. We don't want block dependency...we want the opposite, where we know what the symbols mean. THIS IS HUGE AND POWERFUL. Don't get fooled. It's obvious here. Not so in classes around the country. I have had students in TEARS over this. One 8th grade girl saw me kind of smiling as I looked over her work. "It's not funny! I'm getting an F!" she was hurting, sniffling, crying. "You are going to love or hate me," I said. I knew she would easily understand this because IT WORKS EVERY TIME. Instantly. I love working with kids in algebra because it builds my reputation as a math genius...everybody knows algebra is HARD. I must be a miracle worker if I can take kids from "F" to "A", so quickly, right? Turns out Crewton Ramone isn't magic after all. (Darn it.) After the lesson she was even more pissed off. "Why don't they teach it like this in school!?!" I think there might have been a couple of expletives in there too... She came back with "A's."
Count the big ones first, put them together, only count stuff that's same. Algebra: EASY. What about negative math terms? Then play take away.
"Mathematics should be fun." ~ Peter J. Hilton "But in the new (math) approach, the important thing is to understand what you're doing, rather than to get the right answer." ~ Tom Lehrer Maybe both...
|
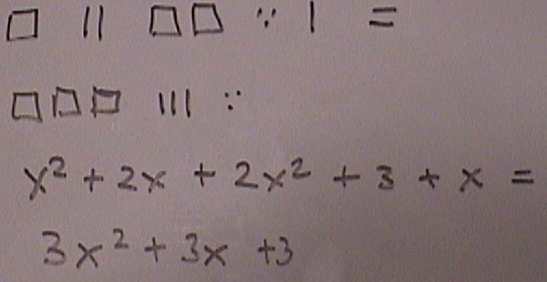
 For little kids the picture is just fun counting...see how we use algebra to teach counting...older kids get to complicate it by calling it "combing like terms" little kids are just counting stuff that's same. The answer is 8x2 + 10x + 12...any little kid can SEE that. In fact it's SO EASY we move right on into factoring polynomials because we can learn even more when we build rectangles combining like terms becomes redundant.
For little kids the picture is just fun counting...see how we use algebra to teach counting...older kids get to complicate it by calling it "combing like terms" little kids are just counting stuff that's same. The answer is 8x2 + 10x + 12...any little kid can SEE that. In fact it's SO EASY we move right on into factoring polynomials because we can learn even more when we build rectangles combining like terms becomes redundant.