Using completing the square to teach counting.

Completing the square is fun and easy, a simple game any student can do. Algebra really is child's play. This can be used with students as young as 4 years of age. First things first, use a three period lesson to introduce x-square, x and a unit. You need to know the names of the pieces or none of this is going to make much sense or be any fun. Go to the concepts page for more on a three period lesson.

x² + x + units

Then ask the student to get out x-squared (x²) and 2x...(you may say 'two exes' for the younger students and evolve to 2x (no "s") as you progress). Form it into a square...what do you need to Complete The Square?

(You may want to back up a little and just build squares [MOD III]  first.)

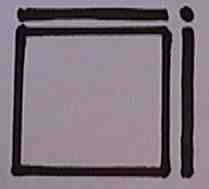
It's visually obvious that a "1" will complete the square. Even in the crude sketch you can see a one will fit in the corner. The rules about what to do when Completing The Square become visually obvious. It's also visually obvious that there are four parts hence the name quadratic.

Of course you divide the coefficient of x by two and then square it...more here for the "advanced" student. 

Next do x² + 4x + 4. But only ask them to get out the x-square, and 4x; they make a square by dividing the 4x into 2x and 2x...We put half of the x's on one side of the rectangle and half on the other, and it becomes visually obvious we'll need 4 to complete the square. But let them discover this. DO NOT DO IT FOR THEM.

Note with the young students we are not even using symbols just verbal commands.

Later they can see this:

x² + 4x + ___

And still later we can set the expression equal to zero and make an equation to solve.

x² + 4x + 4 = 0

It will be easy...the symbols have meaning and the student understands the question. What we are doing is lowering their cognitive load by making them familiar with these simple concepts at an early age.

It means take that equation and turn it into a rectangle and then count one side...and to solve for zero, simply take one side and make it zero. Like this:

x² + 4x + 4 = 0

(x + 2)(x + 2) = 0

x + 2 = 0......x = -2

Understanding hero zero and that 2 - 2 = 0 Is very simple but a very important concept. And now we know that when x = -2, y = 0 written like this:

y = x² + 4x + 4 

[-2, 0]

we can graph this point and talk about x-intercepts and all manner of fun stuff that is lost on the average student because they just learn an algorithm to solve the expression for a test, remember it long enough to pass the class MAYBE and then forget it without ever knowing what completing the square means.

A lot more discussion of the above problems needs to occur. Hero zero needs to come into play, square roots need to be talked about too as well as discussion on degree and quadratics, but for just starting out this about adequate.

If you have a module three password there are quite a few explanatory videos on the next page. Click enter and put your password in.

Enter
(MIII)

Before you go there, if you are working with little kids you may want to watch this video. It shows you how to help them understand number concepts...Identify Squares and Rectangles and count them.

Keep it simple to start.

We are; however, getting way ahead of ourselves, for little kids (and big kids) all we want to do is count the parts of a certain type of rectangle: a square and figure out what completes the square: HENCE THE NAME.

Guess what? The difference of two squares really is the difference of two squares too. I can tell stories about professors on college campuses telling me that they didn't know completing the square meant "completing the square"! In other words they didn't understand that it related to actual geometric figures, they thought Completing The Square was just a cool name that described putting the symbols in the parenthesis.

“Where there is matter, there is geometry.” ~Johannes Kepler, 

We can explain very briefly that it is a tri-nomial, in other words it's made up of three things, the red one, the blue ones and the green ones, orange one or pink ones etc. as the case may be. (Units.) If  explanatations work with little kids they will probably work with learning-disabled children & high school students as well...Keep it simple to start.

Older students may need to hear the formal names, and get an explanation of why a quadratic only has three parts when it comes to the symbols but it's plain to see with the blocks that they do have four parts and that fourth part is what we are "doing" when we are Completing The Square. Most don't care. But it is amazing (to me) that many teachers of mathematics don't even understand why they're called quadratics.

Here we are supposed to be using completing the square to teach counting, but you need to know where the road goes. Next ask them to get out x-square and 6x. By now it's easy and they SEE that 9 will complete the square.

x² + 6x + ___

Again for the little kids this is just a verbal command. Later, after some drawing and three period lessons we can put the symbols on a piece of paper and they can get out the blocks without you telling them what to do. They will be able to "read it." With enough practice they won't even need the symbols written down and will be able to do them in their heads without the blocks or the symbols.

In publik skoolz they call this an oral exam and they rarely ever do them in the "higher" mathematics anymore. After coming to me for just a couple sessions older kids ace the written tests because completing the square is SO FREAKING EASY.  It really is child's play.

Look at how much math is going on here "just" completing the square. 

x² + 6x + 9

For young students when they have to move from the problem x-squared and 2x to x-squared, and 4x they have to figure out they need two more x...simple for adults but for a preschooler/kindergartner this requires a bit of thinking. Then they need two more when they move on to 6x...

x² + 2x + 1 next x² + 4x + 4 next x² + 6x + 9

Getting out four to complete the square, they see that 4 really is square, and that it's two 2s and that x-square, 4x and 4 is a square.

Now they have to move from x-square, 4x and 4 to x-squared and 6x which means they have to get out two more x. Again this requires some thinking for students who are still learning to count and add.

Making 9 into a square allows them to discover 9 is square, and that three 3's is the same as nine: the beginnings of skip counting and multiplication.

Bigger is funner. You might even ask them what the next one is.  I hope you can see in this pattern you will need 8x for the next one. Notice that counting by twos is implied; however, we can also complete the square with odd numbers but that's more advanced. We will also need lessons on squaring numbers that end in five.

I had one young student look at the rectangle and exclaim “I need threes!”

“Good,” I said. “how many is three 3's?”

Pause. “I don't know...a lot.”

“Do you think it's more than ten or less than ten?”

“More.”

“Good, lets find out. Get out a ten for a measuring stick.”

“Opps! It's one less than ten; that mean's it's 9!” GREAT thinking from a 5 year old. Notice: he wasn't wrong just getting more information.

Unspoken is that 10 divided by 3 is 3 with one left over. Also unspoken "NO", "wrong" or any other negative. Remove the NO from the lesson.

We can count three 3's in ten with one left over; the subconscious mind is logging this and we'll bring it up (out) later during a fractions lesson. “To educate” means to draw fourth, not to cram in.

Use math to teach math.

We are using the algebra, specifically completing the square to teach counting...because that's all Basic Math is: counting. Now you know why I am amused by people who really try to sell me on the idea that they are bad at math. All I hear is, "I don't know how to count". But counting is intrinsic to the human.  We do it naturally,

We did the same thing for x² + 8x + ___ and we were Completing The Square with 16.

When I hear "I can't count," they may believe is true but I know it isn't really true, is it?

Now, can you see why I say if you can count to nine, identify a rectangle and tell me whether something is same or different I can teach you math.

Concept #1: Mathematics is the study of numbers and all we can do with numbers is COUNT.

As you can see we again had to measure:

“Four 4's is a lot more than 10!” He exclaimed. “It's ten and 6 more.”

“What's the name for 10 and six?”

“Um...sixteen?”

“Very good.”

The student doesn't even know the names of all his numbers for sure yet! We can still do "algebra."

Can't multiply 4 x 4 yet. We can still do algebra...and as you can see division. There are four 4's in sixteen and further 16 is square and he also discovered that 4 fours is the same as two eights. I didn't tell him these things he "discovered" them for himself. AND we were learning to count by adding two more x.

Explore and discover.

Can you see how this is much more powerful than memorizing math facts, formula or algorithms because he "owns" these concepts and because he discovered them himself; I didn't tell him these things or make him memorize ANYTHING.

I didn't even give an algorithm for solving completing the square problems. Later as we continue on to more "complex" problems like 'what do you do when you only have 3x or 5x'? The student will easily understand what to do. Students who have already been exposed to the symbols and text books suddenly SEE what the algorithm they learned does. (Why did we wait for them to turn 14 before exposing them to completing the square?)

Most know about this much about completing the square: divide the xs by 2, square it and then add the result to the expression or to "both sides" if it's an equation. Suddenly, "complete the square" makes sense because you are. They can see it.

We use the concept of "sameness" and a rectangle being equal to a rectangle on both sides of the equal sign to further deepen this understanding. This is explained on the next page.

Notice how we haven't even mentioned square roots here yet. We can build squares just for fun, and later when we talk about the square roots symbol and what it means; this will also be easy to understand and familiar.

It's also fun to build pyramids with your squares.

We CAN talk about the "factors" when we are completing the square if you like. I usually introduce this concept later with younger students and right away with older students who are learning Completing The Square out of an algebra textbook.

We can count the sides.

The sides on the square below are x plus four and x plus four...it's a square.

It's x plus four squared: (x+4)². We only count things that are same...the blue one is "x" and four units. If we count the bottom of the figure along the edge the distance across the red square on one side is "x" and the bottoms of each of the 4 x's give us four.

In the picture of the expression x² + 8x + 16 we can see the shadow on the bottom even looks like an x + 4.

We count two sides of a rectangle just like we did when we factored 18 with three sixes.

Now if a 5 year old can complete the square, do you think we can get teenagers to “get it” too? The five year old isn't learning algebra per se but he is learning counting, multiplication and division skills. Later when he sees this and is asked to complete the square it is no big deal because he has been playing with it since he was learning how to count. No fear, no tears. It's just algebra. Also I'd like to point out that younger students find it RIDICULOUS that older students think that counting the side of a rectangle or square is hard.

This provides me with endless amusement.

Later we can use a three period lesson to introduce the symbols for these manipulatives as I said earlier.

Then we can use a paper and pencil to give practice problems where the student has to do all the work all by himself: read the symbols get out the blocks and answer the questions. For young children this gives a real sense of accomplishment because as any mother will tell you: children love to say:

“I did it all by myself."

Music to my ears.

ENTER

Use your module three password & click enter for:

• Deepening understanding. 
• Introducing symbols. 
• Factors (x+3)(x+3) = (x+3)² etc
• Solving problems like x² + 6x + 3 = 10 using completing the square. 
• Square root symbol vrs rectangle vrs division symbol.
• Added meaning and conceptual understanding vrs segmented lessons and memorization.

Mind Maps. If you don't know what a "mind map" is, I invite you to search the term in your favorite search engine and watch a couple Youtube clips on it. 

11 Year Old Completes The Square

The idea here is if this 11 year old can do it so can YOU. Also if I can explain it to him you might better explain it to your students and get some ideas.

When I say they don't need the symbols I mean they can hear the problems and do them in their heads...if they have paper and pencil it's even easier. Next lesson we will do similar problems but evaluate the equations for the answers we got so we can really see the squares are equal. Checking your work is always important. Once this habit is formed students always know how well they did on a test because they know if they got it right or not. Ever hear this?:

"How did you do on your test?" "I don't know." How poor must be the understanding to not even know if your answers are correct? 

"How is an error possible in mathematics? A sane mind should not be guilty of a logical fallacy, yet there are very fine minds incapable of following mathematical demonstrations. Need we add that mathematicians themselves are not infallible?" ~Henri Poincaré

GAME/ACTIVITY: If you have a group of four kids you can play a game where you whisper the problem to one student, they write it down, then hand the 'magic formula' to the next student who gets out the blocks, for the student who will build it and the last student draws a picture of it. Banker, Builder Drawer, Recorder. In a classroom situation the teams can race each other to see who can get the most problems done in the allotted time. Some nasty sugary snack like a commercial candy bar filled with chocolate that contains the government allowed roach parts per million makes a fine reward. Kids will kill for this crack.

You might try an apple or an orange but they won't work as hard for these as for processed sugar.

Bonus Videos:

As you can see these lessons really can be done with little, little kids.

Go HOME from Completing The Square.

Go to Passwrod Protected Completeing the Square Page

Square Numbers

"The most extraordinary thing about a really good teacher is that he or she transcends accepted educational methods. Such methods are designed to help average teachers approximate the performance of good teachers." ~Margaret Mead

“The beautiful thing about learning is nobody can take it away from you.” ~B. B. King

“The secret of success is learning how to use pain and pleasure instead of having pain and pleasure use you. If you do that, you're in control of your life. If you don't, life controls you.” ~Anthony Robbins

More math quotes.

Want to see more free pages & lessons & other free stuff on this site?

Consider a dollar a month.

For $1 per month (the lowest level subscription) you get access to
The
Super Duper Super Secret Facebook Page. 
 
You'll find hours and hours of videos with base ten blocks and information you won't may not find anywhere else not even on this website.  I often post video tutoring sessions there. Other people post vids and links there. Lessons cost the people doing them minimum $50.00 and hour. You can watch 2 to 10 of them a month for a dollar...Do the math. Currently 127 people are there. About half of them are active.
You basically get a support group for a buck a month.


Here's My Patreon:

https://www.patreon.com/CrewtonRamone