How to teach Addition
with
Base Ten Blocks

The Addition Course.
Together with this page (the addition page) and these pages (MOD III Password required)
ADDENDS LESSONS
Basic Lessons
Teach Addition
More Addition
You have
No more excuses for getting started!
By the time you scroll to the bottom of this page, if you read the content and watch the videos you should be more than able to teach addition with your base ten blocks.
AND have FUN doing it. Cause no harm.
i teach you by example. You see the concepts in action. Be sure to download the free two page 5 Basic Concepts PDF.
Once you have the Mod III password all the links on this page will be available to you. You won't find the videos and information behind the paywalls anywhere else. i will teach you how to play with purpose.
You will be able to teach addition.
This isn't just as good as teacher training. It is teacher training. Somebody said example isn't a way to to teach: it is the only way to teach. Module III is theory in practice.
 Relax. By the time you finish with this page you'll know how to use base ten blocks to teach addition. Here the student is picturing the blocks he just built in his mind. Imagination is important to develop. "A uniform methodology for the visualization of mathematics".
Relax. By the time you finish with this page you'll know how to use base ten blocks to teach addition. Here the student is picturing the blocks he just built in his mind. Imagination is important to develop. "A uniform methodology for the visualization of mathematics".
Teaching beginner addition is fun. In this methodology, the emphasis will always be on making tens, followed closely by nines...but all numbers can be made up of two other numbers and there are a very finite number of combinations. (45) There is a reason for this: later it will make subtraction, which is just small addition SUPER EASY. It also makes repetitive addition easy because they have a simple algorithm, once they understand all the numbers want to be ten they can add any two single digit numbers.
Playing fun games and activities makes learning addends easy and painless. Worksheets are kept to a bare minimum. Writing and drawing make the activities whole brain exercises.
Absolutely Amazing Addends will show you how and is a great bedtime story book. With bright colors and eye popping graphics your child will enjoy reading this book, print it out or use a tablet, any PDF reader will do.
We start by adding two numbers together up to ten. (9 + 1, 8 + 2 etc.) There are only 25 combinations to master, look closely at the tray pictured below. This is the basis of addition facts mastery. We start in the concrete, that is: with the blocks, and put the student in a situation where they can not fail. Here are some more basic lessons for addition.

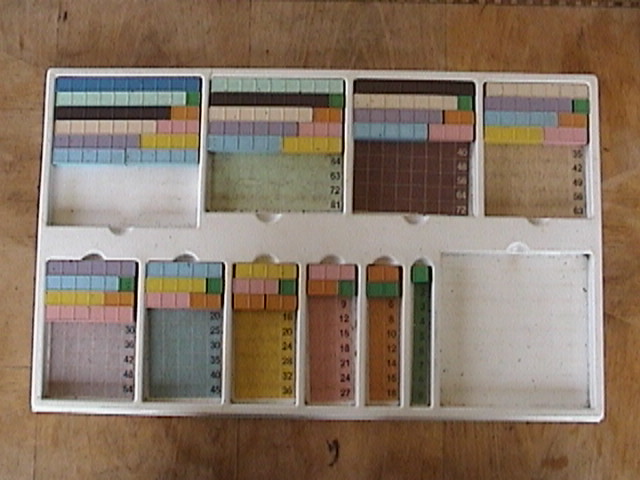 Control of error is intrinsic to the method. Using the top tray to build addends is self correcting.
Control of error is intrinsic to the method. Using the top tray to build addends is self correcting.Addends Make Counting
Fast & Easy
By using a top tray we can begin using numbers to build other numbers. We also make the exercises self correcting this way which again puts the student in a situation where they can not fail; control of error.
Remember: no concept is beyond the grasp of a child if it is presented at the child's level.
This includes using language the child (student) already uses. To start, you don't even have to tell them they are doing addition, or algebra or whatever it is. All we are doing is playing and counting. You don't have to define addition or addends or any of that unless you want to instruct the student in "math vocabulary". (See the Wiki entry below.)
Go here for a taste of some software that helps your student learn to make tens. It uses base ten blocks, it's super easy and FUN for the little ones. It has already been play tested with real pre-schoolers they enjoy it. Check out the I-phone App where all they have to do is touch the screen to identify numbers instead of fool with a mouse which requires manual dexterity and may take away from the focus which is NOT how to use a mouse but how to add numbers together. They start building tens and Nines as well as identify numbers right off.
Then we work our way up past ten...and since we are learning addition why not add the Fibonacci numbers? Also note square roots and Trig being taught at the same time they are learning addends...
Math is a language, and like any language you have to start somewhere but you shouldn't expect to learn it all at once, and you should make it clear to your students that the mathematics is a very large subject but it's not scary or hard, it just takes time to master.
Not everything is going to be understood completely immediately the very first time but over time with the proper methodology it will all start to make sense. If you spend enough time in the land of math eventually you will get the jokes. i need a quote for that...addends are one of the first things to master.
Say, “Make me a 10,” rather than, “and now we are going to learn addition: please commence using the manipulatives to create tens using all the appropriate addends starting from least to greatest using both your left and right hands to facilitate whole brain cognitive learning.”
If you want to get more specific, say ”Watch me.” This is kid speak that works well on adults too. Show them what you want them to do. Watch the videos on this page. Teach by example, learn by example.
IMPORTANT: All students need to learn heir addends including adults and high schoolers especially if they are still counting on their fingers. This is how we are going to get them off their fingers. Don't worry about doing it “wrong.” Just play. Build stuff. Count it. Use the trays.
You can't play math wrong. Okay, maybe some of you could, but you'd have to work at it.
 This exercise is superior to symbols only worksheets in every way. They don't mind the repetition. Repetition is the mother of skill. The more 12s you build the funner it is.
This exercise is superior to symbols only worksheets in every way. They don't mind the repetition. Repetition is the mother of skill. The more 12s you build the funner it is.The exercises should be done using both hands and done relatively quickly. At first it will go slowly but after some repetition it should be a breeze. “Easy smeezy breezy,” as one of my students liked to say. She went from using her fingers to “in her head” in about three lessons. She was about 13 years old at the time, so don't get the idea that these techniques are just for little littles.
In this video we are just playing around, drilling for skills, the mind wants to work fast. Base ten blocks allow you to whip through lots of problems "fast and easy". More fun and better than using symbols only worksheets.
If you can teach a four year old that math is easy you might even be able to teach an adult or even a teen-ager that math really is easy, just like when they were little and math was their favorite subject. i read a study where something crazy like 90% of pre-schoolers thru 1st graders chose MATH as their favorite subject.
The numbers drop off from there and by 4th grade the number is well under 50%. What happened? i'll go into that elsewhere...but long story short: multiplication tables taught at the wrong time. Earlier is better. Also they never learned their addends.
Games And Activities Make Math Fun
. This is usually the first exercise of my class. Make a game of it and race...if you only have one top tray use a stop watch until you have more top trays. You can explain 90% of the math with just the two trays that make up a "combo kit". It's nice to have all the other stuff but you don't absolutely need it and it shouldn't be an excuse for not getting started.
Free Worksheets.
The emphasis is on building tens and nines. This first grade worksheet page for FREE worksheets that help your child master addends for nines and tens. Here is an article Crewton Ramone wrote on The Importance of Addends.
The optimal way to start is in the concrete, then move to drawing, then move to symbols, or as little kids will say drawing the numbers. Often times you will have to mix the ideal order up but start in the concrete. Many students have never seen manipulatives so you have to start with symbols to make them comfortable. Using the familiar symbols first and relating them to the manipulatives puts them at ease. Especially when we get to algebra.
After we build tens, play some math games, sing some math songs give "free time" where you
direct their discovery give some of the building tasks i've listed, (click some of the the links to see more). Then sit back and observe.
Some of the links below require
Building towers and skyscrapers and walls are fun ways to learn what numbers go together to build other numbers. Repetition is the mother of skill, but drudgery and hard tasking makes the student hate the mother. Make it fun and keep it lively. Use 5 minute lessons and change lessons frequently. Having said that, allow students to spend more time if they are interested in a certain game or lesson or activity, but even then don't let them go until they lose interest.
Why not teach addition and place value at the same time? Here is a lesson on place value that shows you how.
Go here for an example of a math activity where we played with and counted oranges for about half an hour...which is a long time for the littler tykes.
Always leave them wanting more. Further, find out (by observing) which games or activities they like best and use those games as rewards for doing exercises they are not as fond of, and remember: each child is unique just like every other child.
Associative & Commutative Properties
You can't talk about addition to teachers and many older students without mentioning The Associative Property of Addition, but skip it when you are working with very young students, unless you just want to practice building "math vocabulary".
Then of course there is The Commutative Property Of Addition ...both are simple no brainer concepts made even easier to explain when you use the blocks and symbols, instead of just symbols.
Here is a page that has actual pictures of worksheets we've done that show some addition concepts represented by drawings and symbols which represent the blocks. This is the first step to understanding that math represents reality numerically, and we can use symbols and pictures to do it. As they get older more symbols less pictures just like when they read they get lots of pictures to start and then move on to books without any pictures at all.
The problem in math is we took the pictures out and forgot to put them back in...we also tend to take the pictures out too early assuming that the student understands. Statements like "the one is understood in the expression x² + 3x + 2" often AREN'T.
In total, there only 45 single digit addends. It is painfully ridiculous that students can get out of high school with out knowing them by heart...or even grade school. Click the link above for free worksheets that you can download so you can begin practicing your nines and tens.
i can't count the number of students i've tutored over the years who were in algebra but were still counting on their fingers for problems like
with multiplication facts that were spotty at best and only went out to 9 x 9, not even 12 x 12. Here we go to 20 x 20.
Learn how to teach addition through play. Use games and activities that are fun and engaging. Using base ten blocks makes learning fun.
Here is a page called "Place Value Made Simple." It shows you how you can use lessons in place value to teach simple addition to young students. It also teaches you how to use the manipulatives to teach place value, of course.
Here is a page from my Blog called "The Importance Of Addends." It talks about just a few of the ways you can use addends and how to teach subtraction; comes with a vid that shows how to use addends to make change for $100.00 and help with the nines times table
Addition
From Wikipedia, the free encyclopedia. [It's full of hypertext, lots of math vocabulary you will never use and fun facts. Some of that vocabulary is needed but I have found many teachers are sure which to emphasize and which gloss over.]
This article is about the mathematical operation. For other uses, see Addition (disambiguation).
3 + 2 = 5 with apples, a popular choice in textbooks[1]
Addition is the mathematical process of putting things together. The plus sign "+" means that numbers are added together. For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples, since 3 + 2 = 5. Besides counts of fruit, addition can also represent combining other physical and abstract quantities using different kinds of numbers: negative numbers, fractions, irrational numbers, vectors, and more.
As a mathematical operation, addition follows several important patterns. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication. All of these rules can be proven, starting with the addition of natural numbers and generalizing up through the real numbers and beyond. General binary operations that continue these patterns are studied in abstract algebra.
Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some animals. In primary education, children learn to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day. Here is the whole Wikipedia entry for "addition."
The dictionary definitions are slightly interesting.
ad·di·tion n.
[From "addition" in The Free Online Dictionary]
1. The act or process of adding, especially the process of computing with sets of numbers so as to find their sum. 2. Something added, such as a room or section appended to a building.
Idioms:
in addition
Also; as well.
in addition to
Over and above; besides.
[Middle English, from Old French, from Latin additi, additin-, from additus, past participle of addere, to add; see add.] ad·dition·al adj.
ad·dition·al·ly adv.
The American Heritage® Dictionary of the EnglishLanguage, Fourth Edition copyright ©2000 by Houghton Mifflin Company. Updated in 2009. Published by Houghton Mifflin Company. All rights reserved.
Addends Past Ten:
45 addends, 400 multiplication facts. These are the addend combinations from 11 to 18. Should be known "by heart" and available for instant recall. They know 7 + 8 is 15, they don't have to think about it or remember it...
addition
Noun
1. the act of adding
2. a person or thing that is added
3. a mathematical operation in which the total of two or more numbers or quantities is calculated
4. in addition (to) besides; as well (as)
additional adj
additionally adv
Collins Essential English Dictionary 2nd Edition 2006 © HarperCollins Publishers 2004, 2006
addition
The act, process, or operation of adding two or more numbers to compute their sum.
The American Heritage® Science Dictionary Copyright © 2005 by Houghton Mifflin Company. Published by Houghton Mifflin Company. All rights reserved.

.Go home from this addition page.

Absolutely Amazing Addends
First Grade Worksheets
Addition And Subtraction And Problem Solving Using Manipulatives
ADDENDS LESSONS

How do you teach addition? Play.
Basic Addition Lessons Up To Ten.
Place Value Made Simple.
(Mod III Password required)
"Without mathematics, there’s nothing you can do. Everything around you is mathematics. Everything around you is numbers".~Shakuntala Devi, Indian writer and mental calculator
"Go down deep enough into anything and you will find mathematics".~Dean Schlicter
"The man who can make hard things easy is the educator". ~Ralph Waldo Emerson
"Nature is written in mathematical language".~Galileo Galilei, Italian astronomer, physicist and engineer
"Mathematics is a language".~Josiah Willard Gibbs, American scientist
"Mathematics is the most beautiful and most powerful creation of the human spirit".~ Stefan Banach, Polish mathematician
Play touches and stimulates vitality, awakening the whole person—mind and body, intelligence and creativity, spontaneity and intuition. ” ~Viola Spolin, American theater coach
Bonus Addition and Subtraction PDF
Here is a bonus PDF for you on addition and subtraction.
Addition and subtraction PDF.
Want to see more free pages & lessons & other free stuff on this site?
Consider a dollar a month.
For $1 per month (the lowest level subscription) you get access to
The
Super Duper Super Secret Facebook Page.
You'll find hours and hours of videos with base ten blocks and information you won't find anywhere else not even on this website there. i often post video tutoring sessions there. Other people post vids and links there too. Lessons cost the people doing them minimum $60.00 and hour. You can watch 2 to 10 of them a month for a dollar...Do the math. Currently 127 people are there. About half of them are active.
You basically get a support group for a buck a month.
Here's My Patreon:
https://www.patreon.com/CrewtonRamone
Note: from time to time the passwords change. Simply e-mail me for a new one or a new passport as the case may be. Annual passes are good for one year, lifetime passes are good for as long as the site remains up, (site has been up for eight years now). All single page passwords have lifetime renewal.
















