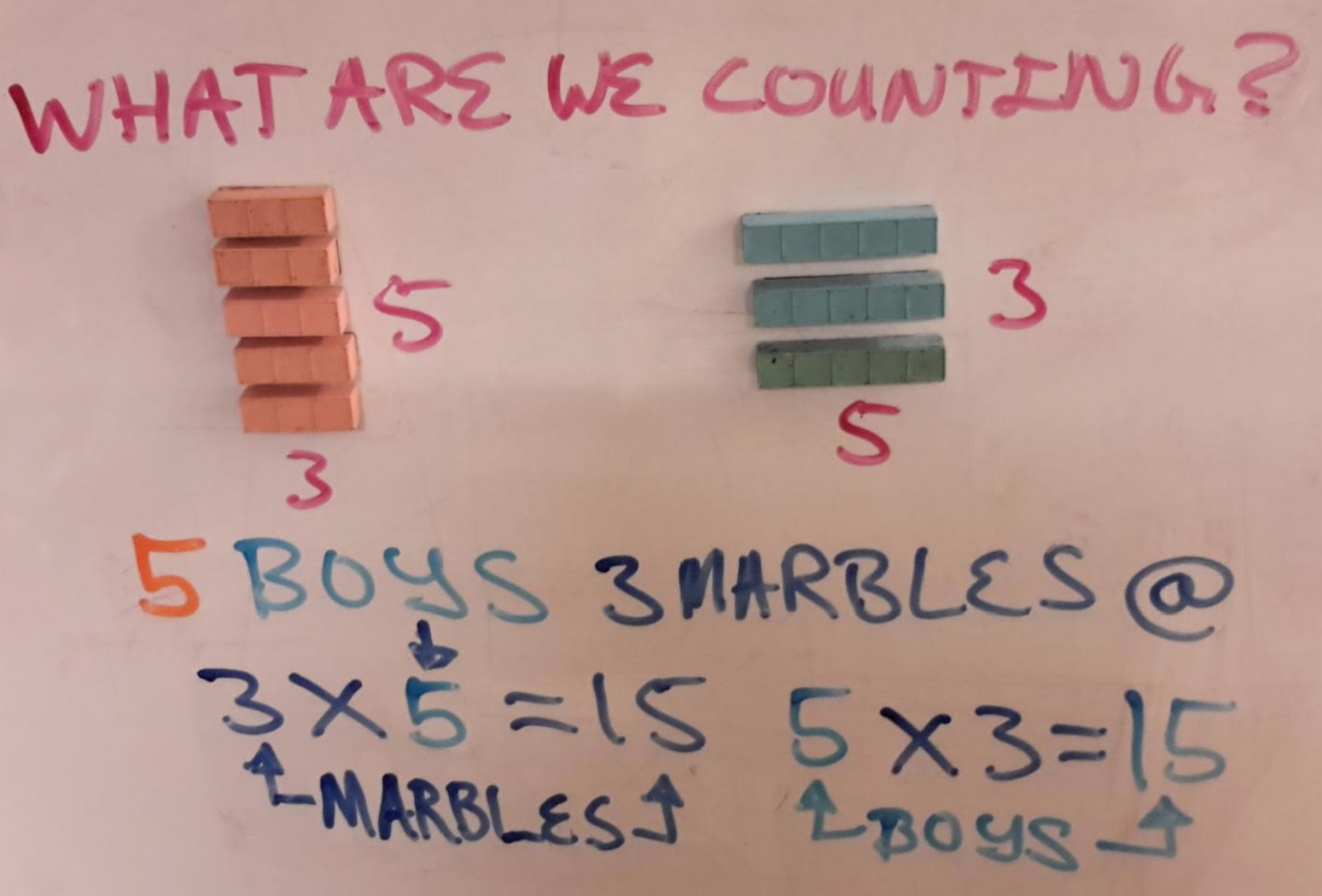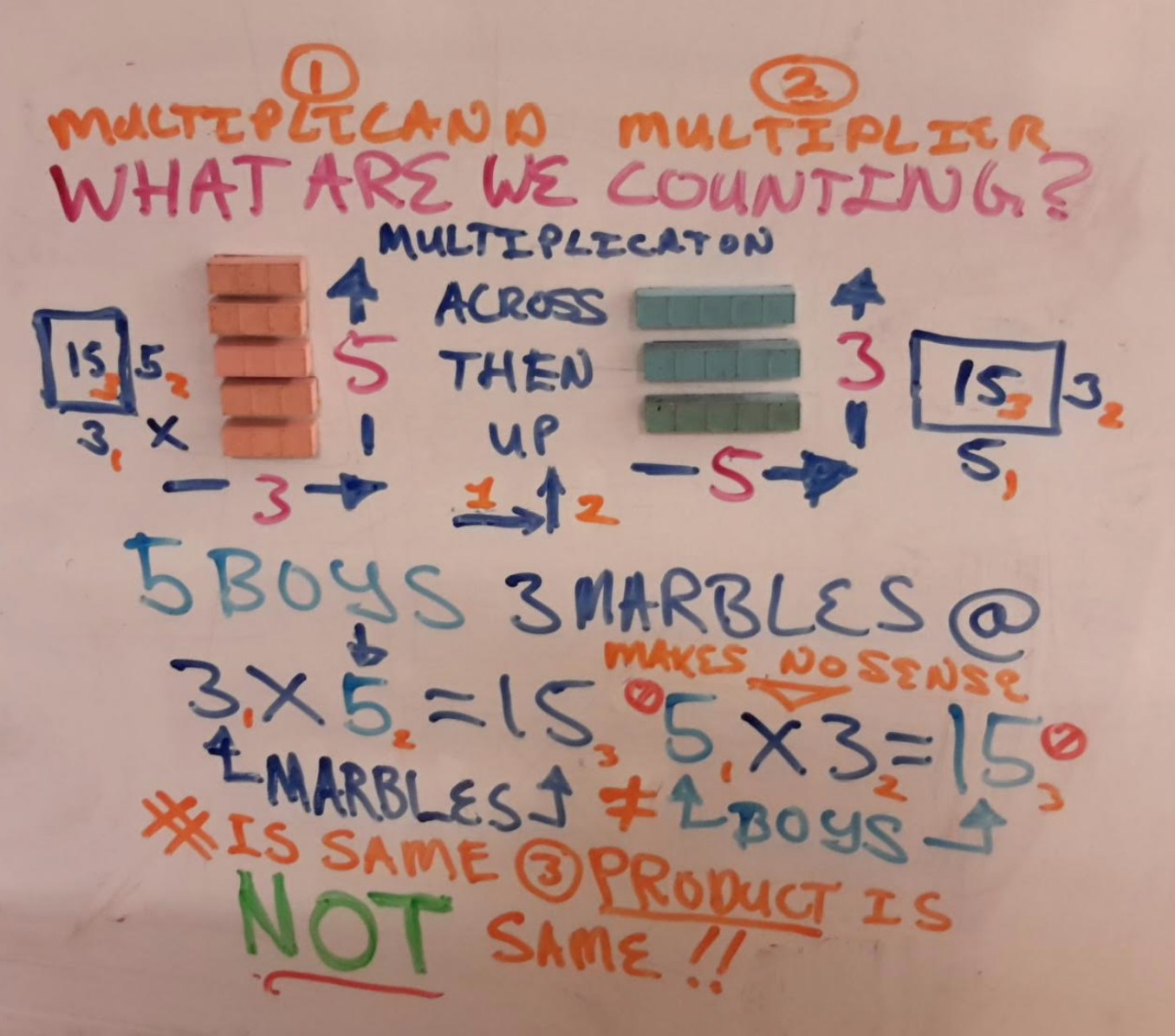Multiplicand and Multiplier

With regard to Multiplicand and Multiplier, first and foremost let me say this: it doesn't really matter which comes first...but using logic and reasoning we can see WHY the multiplicand comes FIRST and the multiplier comes SECOND.

Base ten blocks make it easy to see we are talking about and describing a rectangle. 

Multiplicand, multiplier, product.  ACROSS & UP.  

Dividend, divisor, quotient.   ACROSS & DOWN.

In both cases the thing you are going to operate on comes first then the number of times you are going to count it comes second and the result is either the solution, either product or quotient. How many 5s in 15 is written 15: the thing/amount you are operating on, the dividend, the amount you are starting with, divided by 5 the divisor, the number of times you can count 5 out of 15 is three. 15 ÷ 5 = 3.

Before we go any further in simple terms the multiplicand is the thing being multiplied. The multiplier is the number of times the thing gets multiplied. You can't multiply before you have a thing to multiply. So first what are you multiplying? You will usually even see Multiplicand and Multiplier written in that order...not the other way around.  Because multiplicand comes first. You don't multiply until you have something to multiply, hence multiplicand comes first. Syntax is in fact important.

Five boys three marbles each. 5 x 3 = 15.

Multiplicand and Multiplyer: simple, right? Well no, because you have 15 boys not 15 marbles. The thing being multiplied is marbles. 3 x 5 = 15.

Three marbles five times...You get 15 marbles not 15 boys. Marbles are the multiplicand. The boys are the multiplier. The product is 15 marbles.

But here is some feed back that sums up a discussion i've had in 49 0f 50 states and in one Provence of Canada:

One little comment on what you say here:

"Also be sure to teach them syntax...just let them know that we read 9 x 2 as "nine taken two times" that's two nines as opposed to 2 x 9 which is "two taken nine times" that is, nine twos, subtle difference."

Well, English being what it is, I view 9 x 2 as "nine copies of 2" and 2 x 9 as "2 copies of 9". Just the opposite of the way you teach. And I've seen both "dogmas" taught in various materials. So unfortunately there is no consensus on this.

The person is correct there isn't, but there should be.

First off, these symbols "x" "*" "()()" ALL mean "multiplied by", or "times" they could also mean "copies of" i suppose; however let us go further.

"The Rules" in most countries are very simple, multiplicand first multiplier second. People think it doesn't matter because multiplication is "associative."  Here's a few minutes of explanation:

You might want to go back and watch the whole video just for fun.

Here is a page on the associative property. The Associative and Commutative properties of mathematics and multiplication also seem to add confusion instead of clarity. It's true that multiplication is associative, but associative means 2*(3*4) = (2*3)*4. In this context you want the commutative property, which says 3*5 = 5*3. This is a significant distinction because of the importance of non-abelian groups in math and physics.

In fact, thanks to the internet, i was able to do quite a bit of research on this Multiplicand and Multiplier "argument" or "discussion" if you prefer.

i've had this discussion probably 100 times or more in my travels...consensus is pretty plain: multiplicand first, multiplier second. But "why" is the question i'm much more interested in.

"Any fool can make a rule and any fool will follow..."

5 x 3 is indeed the same as 3 x 5 as long as you stay abstract. These are just factors. i have seen three sets of rules at leaste that I have come across in my travels...the one i espouse here:

1. Multiplicand first, multiplier second.

2. Multiplier first multiplicand second and last.

3. Which ever number is smallest is the multiplier.

10
x130

is considered less correct than

130
x10

But the product, that is, the amount you get after you multiply is the same so why bother even talking about it? Why is there debate? Why is one more/most correct?

Because numbers describe reality numerically that's why, and because syntax matters. WHAT are you multiplying, how many times. he what comes first not the how many. 

The order is universally LxWxH.

Carpenters who stray from this find themselves in trouble, and might end up making doors for some very corpulent midgets.

When using base ten blocks the multiplicand HAS to come first to mimic notation. We count across first, then up. Period. This is the pattern we use. It's the same every time.

But there is more to it than that.

Lets go back to five boys, three marbles each. 3 x 5 or 5 x 3 = 15. What do we have, 15 marbles or 15 boys? Does it matter if we write it 3 x 5? The short answer is NO. We know what the numbers mean from context, we also know what we are counting: we are counting marbles not boys.

The longer answer is yes it does. We have 5 sets of 3 NOT 3 sets of five...this is math NOT English. The way we write 5 sets of 3 is 3 x 5. Three taken five times, five sets of three. The way we show this is with 5 threes, not 3 fives.

Here we have a simple lesson with the blocks that illustrates Multiplicand and Multiplier and also shows the patterning which stays the same throughout this base ten methodology.

One of the reasons we say 3 taken 5 times is because it clarifies that we are doing multiplication. i can tell you with alacrity that there are plenty of school districts teaching multiplication with flashcards where the students think that 3x5 magically turns into 15. And they have to memorize this in order to pass a test. i have seen many students all over the USA express shock and wonder when they see 3 x 5 means 5 threes and that we can count them and see them. Even more so when they SEE division. Some may think i'm exaggerating or just saying this for effect. i'm not.

Multiplicand and Multiplier
made easy:

The students often get concepts confused when they are presented with symbols only. Multiplicand and Multiplier are often terms that get lost in the shuffle if they are discussed at all. Algebra is absolute testament to this. Students are correct that 3x6 is the same as 18. So is 6x3. They think they are synonyms or synonymous , but they lose the concept that we are just counting, or adding over and over again. 11x12 is counting 11 twelve times. There are tricks you can learn for multiplying by 11 and other numbers but don't lose sight of the basic concept: all we are doing is counting, and we are always counting something.

Also we are aware that the pattern for division is always dividend, divisor, quotient. No argument there, in the same manner it's multiplicand, multiplier, product. 

Multiplication as explained by Wikipedia. Somehow I don't think this will help.

Click for an easy explanation of:

Distributive Theory Of Multiplication.

Go from Multiplicand and Multiplier back home. 

Teach Multiplication with base ten blocks.
Crewton Ramone's no mystery theater.
Multiplication Tables
Series A Multiplication Manual

Make multiplication fun with games and activities to aid your students in memorizing multiplication tables.  Remember at the house of math we start early and go out to 20x20, not just 9x9 or 12x12.  Tossing and counting develops patterning but also anchors the multiplication facts multisensorially, the students see hear and feel/touch three sixes and know six times three is 18. They have six (the multiplicand) three times (the multiplier), they can see and hold three sixes which is the same number as six threes but it is visually obvious that they are not the same when it comes to multiplier and multiplicand.  Also if you explain the six is the multiplicand then of course the number of times you toss it is the multiplier...these concepts are easy for any six year old to understand. 

At the early ages language and definitions are still being acquired, and math is often NOT thought of as a language although it is, the mathematics describes reality numerically.  Here are links to many more games an activities to assist you in creating a math rich environment that allows your child to master multiplication tables without tears and misery.  

Multiplication Blog Posts
More Multiplication Activities with Base Ten Blocks

"For any reporter, education is a topic where everything else - money, politics, et cetera - intersects. I have four kids in K through 12, so I'm knee-deep in it. I'm really interested in the philosophy behind it all. Should you just memorize your multiplication tables, or should you understand the concept behind them?" ~Soledad O'Brien

"If everything matters, then nothing matters; if nothing matters then everything matters." ~ The Supreme Yoga

"Biology is the only science in which multiplication means the same thing as division." ~Anonymous

"Beyond the natural numbers, addition, multiplication, and mathematical induction are intuitively clear."~L. E. J. Brouwer

"Collaboration is multiplication." ~John C. Maxwell

Math. Rules.

"The devil is in the details." ~Anon